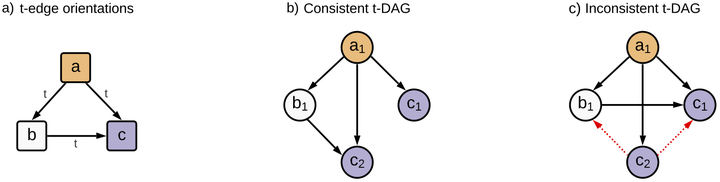
Abstract
Causal discovery from observational data is a challenging task that can only be solved up to a set of equivalent solutions, called an equivalence class. Such classes, which are often large in size, encode uncertainties about the orientation of some edges in the causal graph. In this work, we propose a new set of assumptions that constrain possible causal relationships based on the nature of variables, thus circumscribing the equivalence class. Namely, we introduce typed directed acyclic graphs, in which variable types are used to determine the validity of causal relationships. We demonstrate, both theoretically and empirically, that the proposed assumptions can result in significant gains in the identification of the causal graph. We also propose causal discovery algorithms that make use of these assumptions and demonstrate their benefits on simulated and pseudo-real data.