Abstract
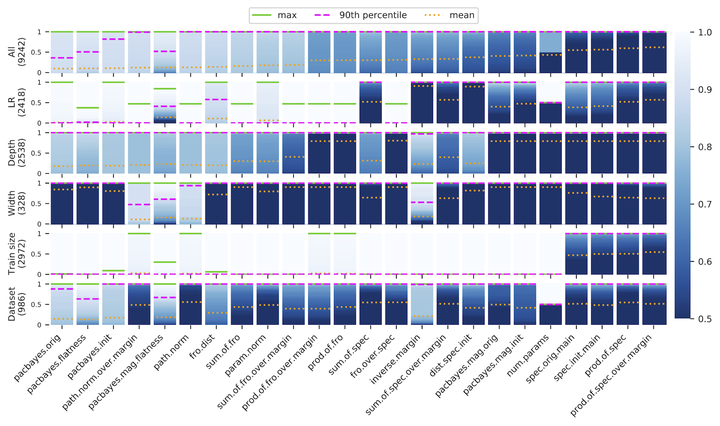
One of the principal scientific challenges in deep learning is explaining generalization, i.e., why the particular way the community now trains networks to achieve small training error also leads to small error on held-out data from the same population. It is widely appreciated that some worst-case theories – such as those based on the VC dimension of the class of predictors induced by modern neural network architectures – are unable to explain empirical performance. A large volume of work aims to close this gap, primarily by developing bounds on generalization error, optimization error, and excess risk. When evaluated empirically, however, most of these bounds are numerically vacuous. Focusing on generalization bounds, this work addresses the question of how to evaluate such bounds empirically. Jiang et al. (2020) recently described a large-scale empirical study aimed at uncovering potential causal relationships between bounds/measures and generalization. Building on their study, we highlight where their proposed methods can obscure failures and successes of generalization measures in explaining generalization. We argue that generalization measures should instead be evaluated within the framework of distributional robustness.